Week 7: Binary Search Trees & Heaps
0.1) What is a BST?
Binary Search Trees (BSTs) are binary trees with the following properties:
- The left subtree of a node (the left child and all of its children) have values less than the parent node
- The right subtree of a node (the right child and all of its children) have values greater than the parent node
- Both the left and right subtrees are also BSTs
BST: Not BST:
4 1
/ \ / \
2 5 2 3
/ \ / \
1 3 4 5
0.2) What Is A Heap?
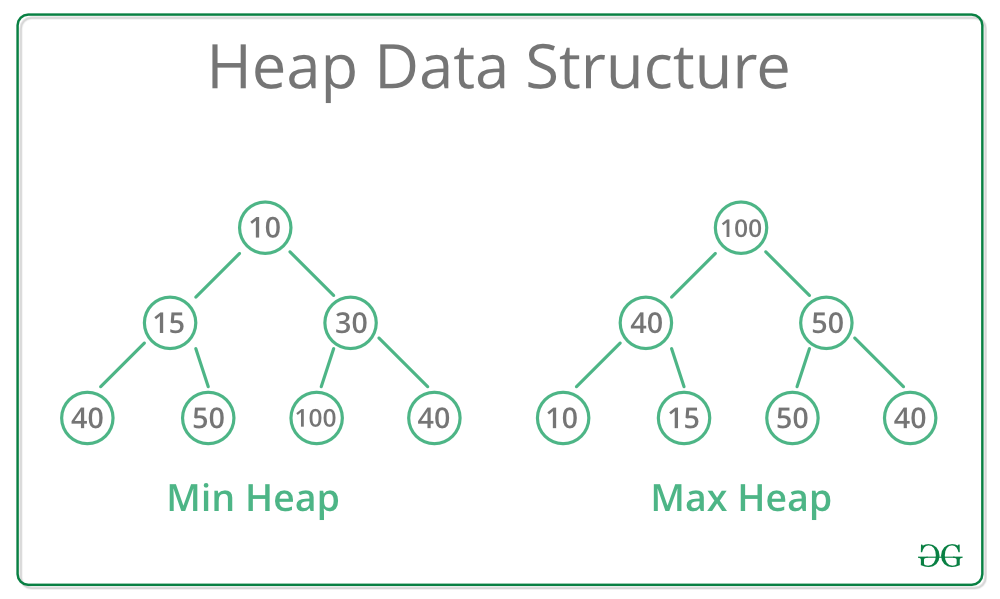
Generally, Heaps can be of two types:
- Max-Heap: In a Max-Heap the key present at the root node must be greatest among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.
- Min-Heap: In a Min-Heap the key present at the root node must be minimum among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.
Main Points:
- Min-heap, Max-heap, Priority-Queue
- Heaps are complete binary trees
- Adding to a heap is O(lgn)
- Removing from root of heap is O(1), BUT YOU NEED TO REHEAPIFY
- Only ever removing from the root of a heap
- Reheapifying is O(lgn)
- size, isEmpty, peek are both O(1)
1) Construct Binary Search Tree from Preorder Traversal
Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.
It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.
A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.
A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.
Example 1:
Input: preorder = [8,5,1,7,10,12]
Output: 8
/ \
5 10
/ \ \
1 7 12
Constraints:
1 <= preorder.length <= 1001 <= preorder[i] <= 1000- All the values of
preorderare unique.
2) Range Sum of BST
Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].
Example 1:
Input:
10
/ \
5 15
/ \ \
3 7 18
root = [10,5,15,3,7,null,18], low = 7, high = 15
Output: 32
Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.
Example 2:
Input:
10
/ \
5 15
/ \ / \
3 7 13 18
/ /
1 6
root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
Output: 23
Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.
Constraints:
- The number of nodes in the tree is in the range
[1, 2 * 10^4]. 1 <= Node.val <= 10^51 <= low <= high <= 10^5- All
Node.valare unique.
3) Relative Ranks
You are given an integer array score of size n, where score[i] is the score of the ith athlete in a competition. All the scores are guaranteed to be unique.
The athletes are placed based on their scores, where the 1st place athlete has the highest score, the 2nd place athlete has the 2nd highest score, and so on. The placement of each athlete determines their rank:
- The
1stplace athlete’s rank is"Gold Medal". - The
2ndplace athlete’s rank is"Silver Medal". - The
3rdplace athlete’s rank is"Bronze Medal". - For the
4thplace to thenthplace athlete, their rank is their placement number (i.e., thexthplace athlete’s rank is"x"). Return an arrayanswerof sizenwhereanswer[i]is the rank of theithathlete.
Example 1:
Input: score = [5,4,3,2,1]
Output: ["Gold Medal","Silver Medal","Bronze Medal","4","5"]
Explanation: The placements are [1st, 2nd, 3rd, 4th, 5th].
Example 2:
Input: score = [10,3,8,9,4]
Output: ["Gold Medal","5","Bronze Medal","Silver Medal","4"]
Explanation: The placements are [1st, 5th, 3rd, 2nd, 4th].
Constraints:
n == score.length1 <= n <= 10^40 <= score[i] <= 10^6- All the values in
scoreare unique.
4) Largest Number After Digit Swaps by Parity
You are given a positive integer num. You may swap any two digits of num that have the same parity (i.e. both odd digits or both even digits).
Return the largest possible value of num after any number of swaps.
Example 1:
Input: num = 1234
Output: 3412
Explanation: Swap the digit 3 with the digit 1, this results in the number 3214.
Swap the digit 2 with the digit 4, this results in the number 3412.
Note that there may be other sequences of swaps but it can be shown that 3412 is the largest possible number.
Also note that we may not swap the digit 4 with the digit 1 since they are of different parities.
Example 2:
Input: num = 65875
Output: 87655
Explanation: Swap the digit 8 with the digit 6, this results in the number 85675.
Swap the first digit 5 with the digit 7, this results in the number 87655.
Note that there may be other sequences of swaps but it can be shown that 87655 is the largest possible number.
Constraints:
1 <= num <= 10^9
5) Trim a Binary Search Tree
Given the root of a binary search tree and the lowest and highest boundaries as low and high, trim the tree so that all its elements lies in [low, high]. Trimming the tree should not change the relative structure of the elements that will remain in the tree (i.e., any node’s descendant should remain a descendant). It can be proven that there is a unique answer.
Return the root of the trimmed binary search tree. Note that the root may change depending on the given bounds.
Example 1:
1 1
/ \ => \
0 2 2
Input: root = [1,0,2], low = 1, high = 2
Output: [1,null,2]
Explanation: 0 is not within the range of 1-2 so it should be removed
Example 2:
3 3
/ \ /
0 4 2
\ => /
2 1
/
1
Input: root = [3,0,4,null,2,null,null,1], low = 1, high = 3
Output: [3,2,null,1]
Explanation: 0 & 4 are not within the range of 1-3 so they should be removed
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. 0 <= Node.val <= 104- The value of each node in the tree is unique.
rootis guaranteed to be a valid binary search tree.0 <= low <= high <= 104