0) What Is A Heap?

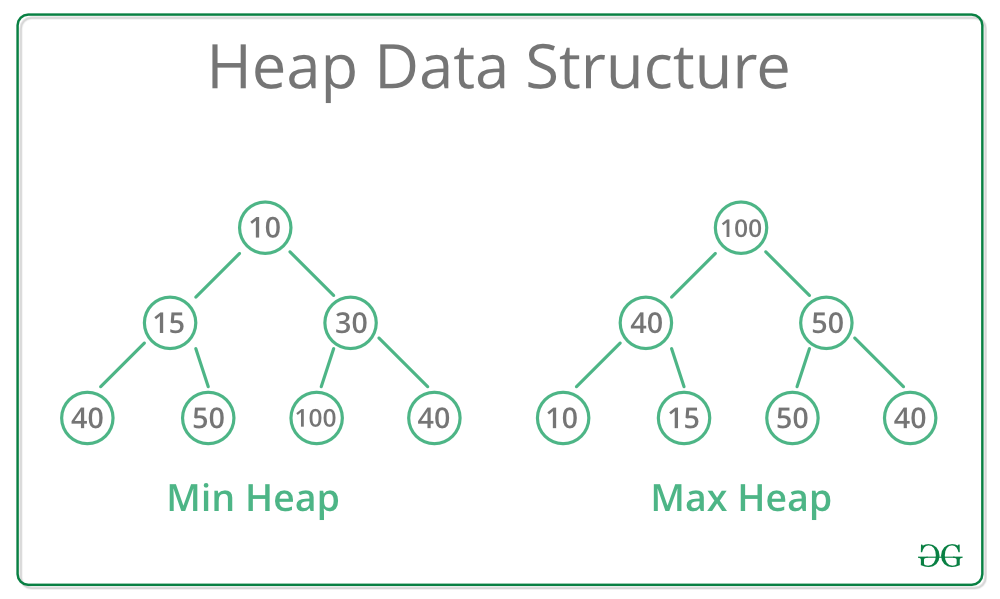
Min Heap and Max Heap

Generally, Heaps can be of two types:

  • Max-Heap: In a Max-Heap the key present at the root node must be greatest among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.
  • Min-Heap: In a Min-Heap the key present at the root node must be minimum among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.

Main Points:

  • Min-heap, Max-heap, Priority-Queue
  • Heaps are complete binary trees
  • Adding to a heap is O(lgn)
  • Removing from root of heap is O(1), BUT YOU NEED TO REHEAPIFY
    • Only ever removing from the root of a heap
  • Reheapifying is O(lgn)
  • size, isEmpty, peek are both O(1)

Learn More

1) Sort an Array Using Heaps

Given an unsorted array of integers, return a sorted array of the same values. You cannot use any of the default sorts. Instead, you must use a heap.

Input: nums = [5,2,3,1]
Output: [1,2,3,5]

Input: nums = [5,1,1,2,0,0]
Output: [0,0,1,1,2,5]

2) Last Stone Weight

You are given an array of integers stones where stones[i] is the weight of the ith stone. Keep on choosing the two heaviest stones and smash them together. If they weigh the same, they are both destroyed. If they have different weights, a smaller stone will be left over, whose weight is the difference of the two larger stones. There will be at most a single stone left at the end of this process. Return the smallest possible weight of that final stone (0 if there are none).

Input: stones = [2,7,4,1,8,1]
Output: 1

Explanation:
We smash 7 and 8 to get 1 so the array converts to [2,4,1,1,1] then,
we smash 2 and 4 to get 2 so the array converts to [2,1,1,1] then,
we smash 2 and 1 to get 1 so the array converts to [1,1,1] then,
we smash 1 and 1 to get 0 so the array converts to [1] then that’s the value of the last stone.

Input: stones = [1]
Output: 1

3) Intersection of Two Arrays

Given two integer arrays nums1 and nums2, return an array of their intersection. Each element in the result must be unique and you may return the result in any order.

Input: nums1 = [1,2,2,1], nums2 = [2,2]
Output: [2]

Input: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
Output: [9,4]

Explanation: [4,9] is also accepted. <!–``` Time Compexity: O(nlgn) // O(n) with hashtables Space Compexity: O(n)



<!-- https://leetcode.com/problems/minimum-number-of-moves-to-seat-everyone/ -->
#### 4) Minimum Number of Moves
You are given two integer arrays (`arr1` and `arr2`), both with length `n`.
Return the smallest number of moves needed to transform `arr2` into `arr1`.

A move is defined to be adding or subtracting `1` from any value in `arr2`.

The elements within `arr2` can be rearranged to whatever order you want (and does not count as a move).

```js
Input: seats = [3,1,5], students = [2,7,4]
Output: 4

Explanation: The students are moved as follows:

  • The first student is moved from from position 2 to position 1 using 1 move.
  • The second student is moved from from position 7 to position 5 using 2 moves.
  • The third student is moved from from position 4 to position 3 using 1 move. In total, 1 + 2 + 1 = 4 moves were used. 
    Input: seats = [2,2,6,6], students = [1,3,2,6]
Output: 4

    Explanation: The students are moved as follows:

  • The first student is moved from position 1 to position 2 using 1 move.
  • The second student is moved from position 3 to position 6 using 3 moves.
  • The third student is not moved.
  • The fourth student is not moved. In total, 1 + 3 + 0 + 0 = 4 moves were used.

5) Distant Barcodes

In a warehouse, there is a row of barcodes, where the ith barcode is barcodes[i].

Rearrange the barcodes so that no two adjacent barcodes are equal. You may return any answer, and it is guaranteed an answer exists.

Input: barcodes = [1,1,1,2,2,2]
Output: [2,1,2,1,2,1]

Input: barcodes = [1,1,1,1,2,2,3,3]
Output: [1,3,1,3,1,2,1,2]